<div dir="rtl" style="text-align: right;" trbidi="on">
[FONT=ge_ss_threeregular][/FONT]
<div dir="rtl" style="-webkit-text-stroke-width: 0px; background-color: white; box-sizing: border-box; color: #666666; font-family: ge_ss_threeregular, 'open sans', sans-serif, arial; font-size: 12px; font-style: normal; font-variant: normal; font-weight: normal; letter-spacing: normal; line-height: 19.2000007629395px; orphans: auto; text-align: right; text-indent: 0px; text-transform: none; white-space: normal; widows: 1; word-spacing: 0px;" trbidi="on"><div style="box-sizing: border-box; text-align: right;" trbidi="on"><div style="box-sizing: border-box; text-align: right;" trbidi="on"><div style="box-sizing: border-box; text-align: right;" trbidi="on">
[FONT=ge_ss_threeregular][/FONT]
<div dir="rtl" style="-webkit-text-stroke-width: 0px; background-color: white; box-sizing: border-box; color: #666666; font-family: ge_ss_threeregular, 'open sans', sans-serif, arial; font-size: 12px; font-style: normal; font-variant: normal; font-weight: normal; letter-spacing: normal; line-height: 19.2000007629395px; orphans: auto; text-align: right; text-indent: 0px; text-transform: none; white-space: normal; widows: 1; word-spacing: 0px;" trbidi="on"><div style="box-sizing: border-box; text-align: right;" trbidi="on"><div style="box-sizing: border-box; text-align: right;" trbidi="on"><div style="box-sizing: border-box; text-align: right;" trbidi="on">
I - INTRODUCTION A L'HYDROLOGIE DE SURFACE
II - LE CYCLE DE L'EAU
-----------------------------------------------
III - LE BASSIN VERSANT
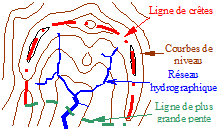
Si le sous-sol est imperméable, le cheminement de l'eau ne sera déterminé que par la topographie. Le bassin versant sera alors limité par des lignes de crêtes et des lignes de plus grande pente comme le montre la figure ci-jointe.
https://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullIII.1.2 - Bassin versant hydrogéologique
L'utilisation de caractéristiques morphométriques a pour but de condenser en un certain nombre de paramètres chiffrés, la fonction h = f (x,y) à l'intérieur du bassin versant (h altitude, x et y coordonnées d'un point du bassin versant). Nous utiliserons trois types différents de paramètres morphométriques.
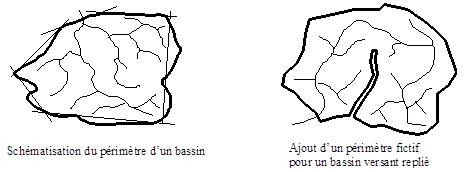
Le périmètre est curvimétré sur carte cartographique mais, selon l'échelle de la carte, les détails sont plus ou moins nombreux et il en résulte des différences de mesures. Par ailleurs, on devrait souvent prendre en compte des détails de la frontière qui, on s'en rend compte intuitivement, n'ont aucune influence sur l'écoulement. Avant de procéder au curvimétrage, il faut donc procéder à une schématisation des limites du bassin, soit par des courbes à grand rayon de courbure, soit par un tracé polygonal.
Dans des cas particuliers tels que celui d'un bassin replié sur lui-même, on pourra être amené à tracer des contours fictifs qui tiendront compte de chaque cas particulier.
Le périmètre P n'est généralement pas utilisé directement mais le plus souvent à travers des valeurs qui en dérivent, comme la "longueur L du rectangle équivalent". On définit le rectangle équivalent comme le rectangle de longueur L et de largeur l qui a même surface et même périmètre que le bassin versant, soit à l'aide de :
P = 2 . (L + l) et A = L . l
L'inconvénient de cette méthode est que l'on peut rencontrer des bassins plus compacts qu'un carré ; l'équation n'a alors plus de racines réelles !
A la suite de ces remarques critiques sur l'utilisation du périmètre comme critère de longueur, il a fallu définir d'autres caractéristiques et en particulier :
- la "longueur du plus long thalweg" (lt). Cette caractéristique n'amène guère de remarques si ce n'est que dans la plupart des cas, on admet qu'il faut poursuivre le thalweg indiqué sur les cartes topographiques, vers l'amont jusqu'à la limite du bassin. De même, si le cours aval présente des méandres, on curvimètre en général tous les méandres.
- la "distance de l'exutoire au centre de gravité du bassin" (lg). Ceci paraît être une bonne caractéristique de longueur mais elle nécessite l'évaluation de la position du centre de gravité du bassin ;
- la "plus grande longueur entre deux points de la frontière" (L). On utilise cette caractéristique surtout en association avec la "plus grande largeur" (l) perpendiculaire à la plus grande longueur. La caractéristique de forme la plus utilisée est le "coefficient Kc de Gravelius". Il se définit comme le rapport du périmètre du bassin versant au périmètre du cercle ayant même surface (appelée aussi coefficient de capacité) :
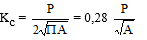
A : surface et P : périmètre du bassin versant
On utilise également pour caractériser la forme d'un bassin, son "rectangle équivalent" (défini plus haut) et le rapport de la plus grande longueur à la plus grande largeur perpendiculaire (voir plus haut).
Enfin, une des façons des plus sophistiquées (mais des plus pénibles) pour caractériser la disposition d'un bassin dans le plan est d'établir la courbe aire-distance. Cette courbe donne la surface s en km2 (ou en %) qui se trouve à une distance hydraulique supérieure à une valeur donnée d. (La distance hydraulique est la distance parcourue par une particule d'eau qui ruisselle d'un point du bassin jusqu'à l'exutoire.)
https://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullIII.2.2 - Caractéristiques des altitudes (hypsométrie)
En général, on ne s'intéresse pas à l'altitude moyenne mais plutôt à la dispersion des altitudes.
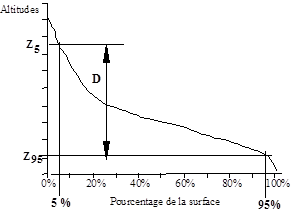
L'étude statistique permet de tracer la "courbe hypsométrique".Cette courbe donne la surface s (en km2 ou en % de la surface totale) où les altitudes sont supérieures à une cote h donnée Cette courbe est établie en planimétrant pour différentes altitudes les surfaces situées au-dessus de la courbe de niveau correspondante. Cette méthode est précise mais fastidieuse. Une autre consiste à échantillonner les altitudes selon un maillage carré. On admet alors que l'altitude au centre d'une maille est égale à l'altitude moyenne de la maille.
Bien souvent, on définit la "dénivelée D"comme étant la différence de cote entre H5 % et H95 % : D = H5 % - H95 %
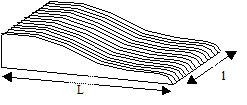
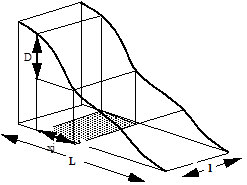
Parfois, on schématise la forme du bassin et la répartition des altitudes sur le rectangle équivalent. On construit alors une surface ayant même hypsométrie, même périmètre et même surface que le bassin versant.
https://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullIII.2.3 - Les indices de pente
L'objet de ces indices est de caractériser les pentes d'un bassin et de permettre des comparaisons et des classifications.
https://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullIII.2.3.1 – La pente moyenne
L'idée première qui vient à l'esprit est de caractériser les pentes par leur valeur moyenne I pondérée par les surfaces.
Soit D l'équidistance des courbes de niveau, soit dj la largeur moyenne de la bande j comprise entre les lignes de niveau j et j+1 et soit li la longueur moyenne de cette bande. La pente moyenne nj sur cette bande est :
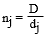
La surface de la bande j est : dj . lj = aj
La pente moyenne I pondérée par les surfaces est donc
Si Lc est la longueur totale des courbes de niveau équidistante de D, la pente moyenne I a pour expression :
L'estimation de cette expression simple est cependant laborieuse puisqu'il faut curvimétrer toutes les courbes de niveau. Ceci explique que cet indice est peu utilisé dans la pratique.
https://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullIII.2.3.2 - Indice de pente de Roche Ip
m. roche a proposé un indice de pente plus facile à calculer que le précédent : Ip est la moyenne de la racine carrée des pentes mesurées sur le rectangle équivalent, et pondérée par les surfaces.
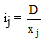La pente moyenne i sur la bande j est :
La surface de cette bande est : aj = lj xj
d'où l'expression :
En posant bj le pourcentage de la surface totale se trouvant entre hj+1 et hj :
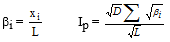
L'indice de Roche étant cependant trop long à évaluer pour des études rapides, on a proposé un indice encore plus simple : la pente globale...
<div style="box-sizing: border-box; text-align: right;"><div style="box-sizing: border-box; text-align: right;"><span style="box-sizing: border-box; font-family: Times, serif; font-size: 9.5pt;">IgII - LE CYCLE DE L'EAU
-----------------------------------------------
III - LE BASSIN VERSANT
En tout point d'un cours d'eau, nous serons amenés à définir son bassin versant et à caractériser son comportement hydrologique
III.1 - Notion de "Bassin Versant"
https://www.blogger.com/null
Le bassin versant en une section d'un cours d'eau est défini comme la surface drainée par ce cours d'eau et ses affluents en amont de la section. Tout écoulement prenant naissance à l'intérieur de cette surface doit donc traverser la section considérée, appelée exutoire, pour poursuivre son trajet vers l'aval.
Selon la nature des terrains, nous serons amenés à considérer deux définitions.
III.1.1 - Bassin versant topographiqueIII.1 - Notion de "Bassin Versant"
https://www.blogger.com/null
Le bassin versant en une section d'un cours d'eau est défini comme la surface drainée par ce cours d'eau et ses affluents en amont de la section. Tout écoulement prenant naissance à l'intérieur de cette surface doit donc traverser la section considérée, appelée exutoire, pour poursuivre son trajet vers l'aval.
Selon la nature des terrains, nous serons amenés à considérer deux définitions.
Si le sous-sol est imperméable, le cheminement de l'eau ne sera déterminé que par la topographie. Le bassin versant sera alors limité par des lignes de crêtes et des lignes de plus grande pente comme le montre la figure ci-jointe.
https://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullIII.1.2 - Bassin versant hydrogéologique
Dans le cas d'une région au sous-sol perméable, il se peut qu'une partie des eaux tombées à l'intérieur du bassin topographique s'infiltre puis sorte souterrainement du bassin (ou qu'à l'inverse des eaux entrent souterrainement dans le bassin).
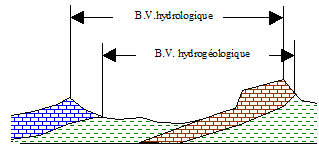
Dans ce cas, nous serons amenés à ajouter aux considérations topographiques des considérations d'ordre géologique pour déterminer les limites du bassin versant. Cette distinction entre bassin topographique et hydrogéologique se justifie surtout pour les petits bassins. En effet, lorsque la taille du bassin augmente, les apports et les pertes souterraines ont plus de chance de se compenser. De plus, on peut admettre que le débit des cours d'eau est proportionnel à la surface du bassin, les échanges souterrains se font, eux, aux frontières et varient donc sensiblement comme le périmètre. Lorsque la taille du bassin augmente, la surface croît plus vite que le périmètre et la valeur relative des échanges souterrains par rapport au débit de surface tend à devenir négligeable.
III.2 - Caractéristiques morphométriques
Dans ce cas, nous serons amenés à ajouter aux considérations topographiques des considérations d'ordre géologique pour déterminer les limites du bassin versant. Cette distinction entre bassin topographique et hydrogéologique se justifie surtout pour les petits bassins. En effet, lorsque la taille du bassin augmente, les apports et les pertes souterraines ont plus de chance de se compenser. De plus, on peut admettre que le débit des cours d'eau est proportionnel à la surface du bassin, les échanges souterrains se font, eux, aux frontières et varient donc sensiblement comme le périmètre. Lorsque la taille du bassin augmente, la surface croît plus vite que le périmètre et la valeur relative des échanges souterrains par rapport au débit de surface tend à devenir négligeable.
L'utilisation de caractéristiques morphométriques a pour but de condenser en un certain nombre de paramètres chiffrés, la fonction h = f (x,y) à l'intérieur du bassin versant (h altitude, x et y coordonnées d'un point du bassin versant). Nous utiliserons trois types différents de paramètres morphométriques.
https://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullIII.2.1 - Caractéristiques de la disposition dans le plan
III.2.1.1 - Surface A
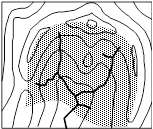
La surface du bassin versant est la première et la plus importante des caractéristiques. Elle s'obtient par planimétrage sur une carte topographique après que l'on y ait tracé les limites topographiques et éventuellement hydrogéologiques. La surface A d'un bassin s'exprime généralement en km2.
file:///C:/Users/RIRAKH~1/AppData/Local/Temp/msohtmlclip1/01/clip_image002.gif
https://www.blogger.com/null
III.2.1.2 – Longueur
On utilise différentes caractéristiques de longueur ; la première et une des plus utilisées est le "périmètre P du bassin versant".
III.2.1.1 - Surface A
La surface du bassin versant est la première et la plus importante des caractéristiques. Elle s'obtient par planimétrage sur une carte topographique après que l'on y ait tracé les limites topographiques et éventuellement hydrogéologiques. La surface A d'un bassin s'exprime généralement en km2.
file:///C:/Users/RIRAKH~1/AppData/Local/Temp/msohtmlclip1/01/clip_image002.gif
https://www.blogger.com/null
III.2.1.2 – Longueur
On utilise différentes caractéristiques de longueur ; la première et une des plus utilisées est le "périmètre P du bassin versant".
Le périmètre est curvimétré sur carte cartographique mais, selon l'échelle de la carte, les détails sont plus ou moins nombreux et il en résulte des différences de mesures. Par ailleurs, on devrait souvent prendre en compte des détails de la frontière qui, on s'en rend compte intuitivement, n'ont aucune influence sur l'écoulement. Avant de procéder au curvimétrage, il faut donc procéder à une schématisation des limites du bassin, soit par des courbes à grand rayon de courbure, soit par un tracé polygonal.
Dans des cas particuliers tels que celui d'un bassin replié sur lui-même, on pourra être amené à tracer des contours fictifs qui tiendront compte de chaque cas particulier.
Le périmètre P n'est généralement pas utilisé directement mais le plus souvent à travers des valeurs qui en dérivent, comme la "longueur L du rectangle équivalent". On définit le rectangle équivalent comme le rectangle de longueur L et de largeur l qui a même surface et même périmètre que le bassin versant, soit à l'aide de :
P = 2 . (L + l) et A = L . l
L'inconvénient de cette méthode est que l'on peut rencontrer des bassins plus compacts qu'un carré ; l'équation n'a alors plus de racines réelles !
A la suite de ces remarques critiques sur l'utilisation du périmètre comme critère de longueur, il a fallu définir d'autres caractéristiques et en particulier :
- la "distance de l'exutoire au centre de gravité du bassin" (lg). Ceci paraît être une bonne caractéristique de longueur mais elle nécessite l'évaluation de la position du centre de gravité du bassin ;
- la "plus grande longueur entre deux points de la frontière" (L). On utilise cette caractéristique surtout en association avec la "plus grande largeur" (l) perpendiculaire à la plus grande longueur. La caractéristique de forme la plus utilisée est le "coefficient Kc de Gravelius". Il se définit comme le rapport du périmètre du bassin versant au périmètre du cercle ayant même surface (appelée aussi coefficient de capacité) :
A : surface et P : périmètre du bassin versant
On utilise également pour caractériser la forme d'un bassin, son "rectangle équivalent" (défini plus haut) et le rapport de la plus grande longueur à la plus grande largeur perpendiculaire (voir plus haut).
Enfin, une des façons des plus sophistiquées (mais des plus pénibles) pour caractériser la disposition d'un bassin dans le plan est d'établir la courbe aire-distance. Cette courbe donne la surface s en km2 (ou en %) qui se trouve à une distance hydraulique supérieure à une valeur donnée d. (La distance hydraulique est la distance parcourue par une particule d'eau qui ruisselle d'un point du bassin jusqu'à l'exutoire.)
https://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullIII.2.2 - Caractéristiques des altitudes (hypsométrie)
En général, on ne s'intéresse pas à l'altitude moyenne mais plutôt à la dispersion des altitudes.
L'étude statistique permet de tracer la "courbe hypsométrique".Cette courbe donne la surface s (en km2 ou en % de la surface totale) où les altitudes sont supérieures à une cote h donnée Cette courbe est établie en planimétrant pour différentes altitudes les surfaces situées au-dessus de la courbe de niveau correspondante. Cette méthode est précise mais fastidieuse. Une autre consiste à échantillonner les altitudes selon un maillage carré. On admet alors que l'altitude au centre d'une maille est égale à l'altitude moyenne de la maille.
Bien souvent, on définit la "dénivelée D"comme étant la différence de cote entre H5 % et H95 % : D = H5 % - H95 %
Parfois, on schématise la forme du bassin et la répartition des altitudes sur le rectangle équivalent. On construit alors une surface ayant même hypsométrie, même périmètre et même surface que le bassin versant.
https://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullIII.2.3 - Les indices de pente
L'objet de ces indices est de caractériser les pentes d'un bassin et de permettre des comparaisons et des classifications.
https://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullIII.2.3.1 – La pente moyenne
L'idée première qui vient à l'esprit est de caractériser les pentes par leur valeur moyenne I pondérée par les surfaces.
Soit D l'équidistance des courbes de niveau, soit dj la largeur moyenne de la bande j comprise entre les lignes de niveau j et j+1 et soit li la longueur moyenne de cette bande. La pente moyenne nj sur cette bande est :
La surface de la bande j est : dj . lj = aj
La pente moyenne I pondérée par les surfaces est donc
L'estimation de cette expression simple est cependant laborieuse puisqu'il faut curvimétrer toutes les courbes de niveau. Ceci explique que cet indice est peu utilisé dans la pratique.
https://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullIII.2.3.2 - Indice de pente de Roche Ip
m. roche a proposé un indice de pente plus facile à calculer que le précédent : Ip est la moyenne de la racine carrée des pentes mesurées sur le rectangle équivalent, et pondérée par les surfaces.
La pente moyenne i sur la bande j est : La surface de cette bande est : aj = lj xj
d'où l'expression :
En posant bj le pourcentage de la surface totale se trouvant entre hj+1 et hj :
L'estimation de Ip est plus simple que celle de I puisque l'on travaille sur le rectangle équivalent. Par ailleurs, la valeur de I est peu affectée par le choix de D (une dizaine de classes suffit pour bien estimer Ip).
https://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullhttps://www.blogger.com/nullIII.2.3.3 - Indice de pente globale Ig
L'indice de Roche étant cependant trop long à évaluer pour des études rapides, on a proposé un indice encore plus simple : la pente globale...
D étant la dénivelée h5 % - h95 %, définie sur la courbe hypsométrique ou même directement à l’œil sur la carte topographique ; L étant la longueur du rectangle équivalent.
Cet indice, très facile à calculer, est des plus utilisés. Il sert de base à une des classifications O.R.S.T.O.M. pour des bassins versants dont la surface est des l'ordre de 25 km2 :